활성 모형

 게시글 보기 도움말: 데스크톱, 크롬, 제이위키 벡터 스킨 베이스 | 제작: Ernst | 세계관: 이뮨 신화

픽션. 본 문서는 허구의 내용으로 이루어져 있습니다. 제이위키는 창작 · 설정 위키로 현실과는 무관한 정보들이 다수이며 본 문서 또한 그 중 하나입니다. 설정 및 창작물 또한 저작권법에 적용을 받으므로 인용과 편집, 이용에 유의해 주십시오.

이뮨론

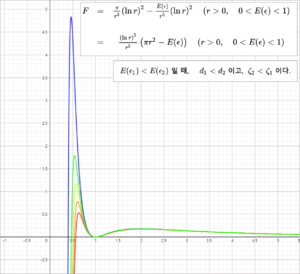이넴-아덴 염사력 그래프 (각각 하나의 이넴과 아덴 간에 작용하는 힘의 이상총량)
이뮨상태학
기본 개념	이뮨 · 에겐 (이넴 · 아덴) · 염사력
활성 이론	비활성 모형 · 준활성 모형 · 활성 모형 · 과활성 모형
구조 이론	공명 · 공유 구조화 (격자 모형 · 다차원 모형) · 존재 모순 · 결합 붕괴 · 매개 입자 가설
각성론	각성 · 상위 각성 · 실체화 이론
실용 이론	자유 인자 · 실질 인자 · 상호 변환 메커니즘
이뮨차원학
이성체계론	에논 가설 · 공유연산성 · 통합연산성 · 에너지교환 메커니즘
원소에너지학	활성도 이론 · 하렌 간섭 · 축력 꼬임 이론 · 축력 꼬임 이론 (축력 형상 · 복합 축력 형상) · 이뮨-에너지 변환
이뮨장 이론	단일망 메커니즘 · 차원망 교차점 가설 · 터널 현상 · 공유 거리 · 한계 변형점
이뮨파괴론	에제스의 문 (에제스 확률 ㆍ 상위 차원 가설) · 브레탈 복구 회로 · 비파괴 소멸 메커니즘
이뮨합론	각성 흡수 · 단일 실체화 · 합일론
동화 이론	이뮨 동화 현상 · 원소시초론 · 선-의지 가설 · 불가분 다원소론
이뮨마도학
작재론	원소 유도 · 자유원소재배열 · 자유원소동화법 · 원소생성법
가동론	원소 유화 · 원소 초유화 · 간접 제어론 · 변환 제어론
기타	마학 · 가호 · 마법론 · 이뮨 심접
입자
스탠다드	이뮤 · 이뮤니네스 · 이뮤니데스 · 이뮤니아스 · 이뮤니스 · 이뮤니아
익스펜션	이뮤니온 · 이뮤니우스 · 이뮤니르 · 이뮤니폰 · 이뮤니엔
에핌	에피힘 · 에피스 · 에피켐 · 에피놈 · 에피람
하르마	리하겐 · 하르겐 · 베하겐 · 크라옴 · 텐비르 · 헬리논 · 라겐 · 스필라 · 아쿠논
샤넨	아르탈 · 브레탈
리카	리아메르논 · 이데헤르논
카논	쉴리아 · 퀼리아
리케	이터니움 · 서케니움 · 뫼르비움

활성 모형(活性, 영어: active model) 또는 활모형(活模型), 이루네이트(

, 영어: iruneit)는 해당 이뮨에서 원소역학적인 계에서 양자적 최소 에너지량 이상을 가지는 불안정 상태이다. 이 모형에 이르기 위해서는 일정한 고유값 이상의 에너지 공급이 필요하며 이때 그 고유값을 활성에너지라 부르며 이 값은 비활성 에너지나 준활성 에너지와는 달리 에겐의 에너지활성평균값에 따라 크게 변하는 특징이 있다. 지속적인 에너지 공급이 없다면 준활성 상태로 돌아가는 등 들뜬 상태와 비슷하며 불안정하다고 말할 수 있다. 에겐이 활발히 활동하며 한계변형점 안에서 구조체 확장과 변형을 일으키고 상위 의식체계에 기반한 자아의식을 가진다.

붉은색 그래프 에너지활성평균이 큰 그래프;	노랑색 그래프 에너지활성평균이 중간인 그래프;	파랑색 그래프 에너지활성평균이 작은 그래프;		볼로쿰 공식으로 알려져 있는 에겐 간 에너지 관계를 나타내는 식과 경향성을 정리한 것이다. E(ε) : 활성에너지평균값; ζ : 활성에너지; r , d : 거리값 F : 상태유지비용 (에너지)
볼로쿰 공식에 따른 기본 그래프, 색으로 칠해진 거리 값이 활성 모형에 해당하는 거리값 근사치이다.

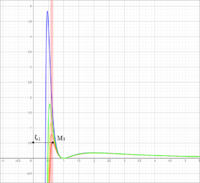
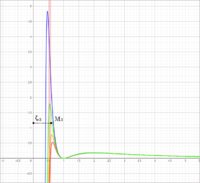
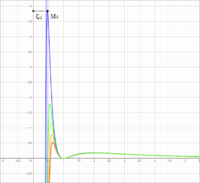
이뮨구조학적으로 활성 모형은 볼로쿰 공식에서 첫번째 근부터 첫번째 극대값^점M까지의 거리값 만큼 두 에겐이 떨어져 있을 경우의 상태이다. 이 때 볼로쿰 공식의 세로축(에너지) 값이 매우 높아짐으로 매우 불안정적이다. 다시 말해, 활성 모형에 들어선 이뮨은 모형을 유지하는데 외부의 상당량의 에너지를 필요로 한다는 것이다.

이러한 구조적인 특징 때문에 교차성을 띠며 이를 통해 상위 의식체계를 확보할 수 있다. 이 교차 부분을 교차특이점이라고 부르며 관측은 불가능에 가깝다. 이러한 의식체계는 준활성 모형과 비슷하게 구조체와 망을 통해 연산 공유가 가능하며 자아 간의 교류를 통해 자아성을 강화한다.